Two Pointer

Two pointers iterate through the data structure in tandem until one or both of the pointers hit a certain condition.

Two pointers are needed because with just pointer, you would have to continually loop back through the array to find the answer, giving O(n²) time.

Usually this approach is of O(n) time complexity.

When to use

1. Input is an Array or Linked List.
2. Find pairs/triplets with certain sums.
3. Detect cycles.
4. Check palindromes.
5. Compare two elements.
6. Optimizing a nested loop solution to O(1) solution
7. Move an element from one position to another in an array
8. Searching pairs in a sorted array or linked list
9. Optimizing comparisons to get better than O(n²) time
10. Find a set of elements that fulfill certain constraints
11. The set of elements in the array is a pair, a triplet, or a subarray
12. Find intersections between two data structures
13. Find middle of a linked list.
14. Find cycle in linked list.

Methodology

1. A single loop with two pointers within the loop

int j = 0;
for (int i = 1; i < nums.size(); i++) {
	if (nums[i] != nums[j]) {
		...
	}
}

Forms

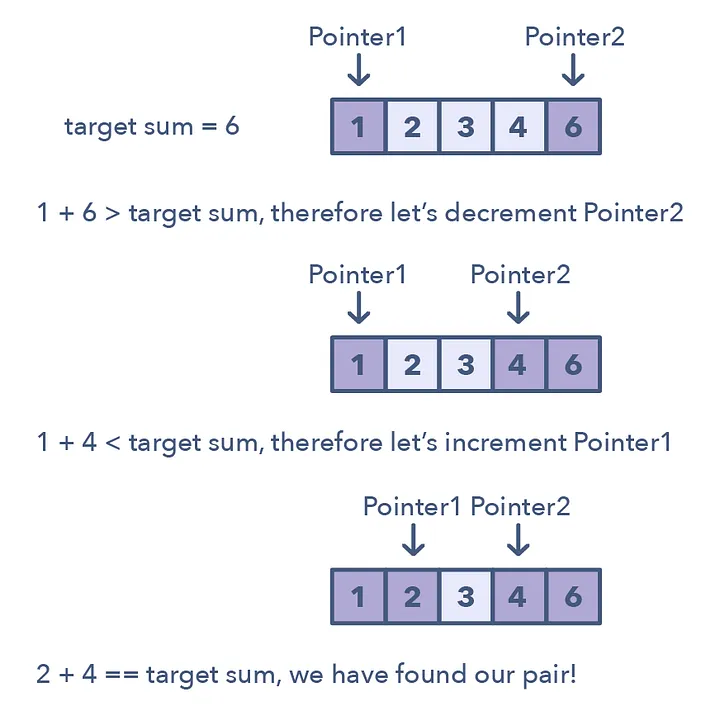
Front & Back

1. Sort the array (if order doesn’t matter)
2. One pointer starts from the front of the array
3. The other pointer starts from the back of the array
4. Moving inward depending on the sum or condition
5. Usually stopping the loop before both pointers equal one another
   1. while(left < right)
   2. while(right > left)

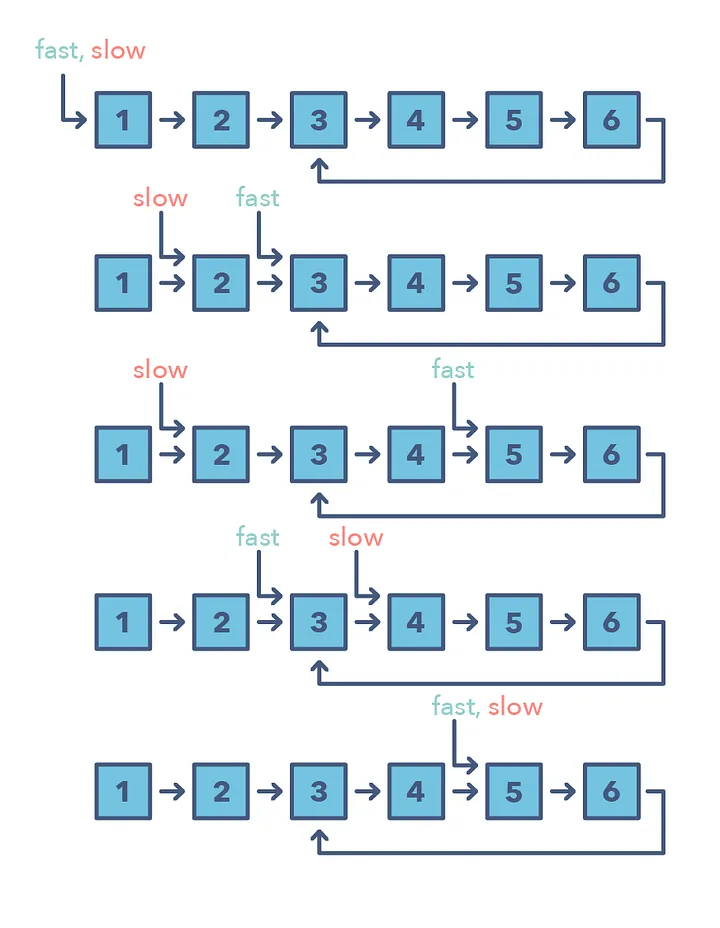
Slow & Fast (Floyd’s Cycle Detection)

1. One pointer starts from the first element, this is the slow pointer
2. The other pointer starts from the second element, this is the fast pointer
3. Fast pointer usually moves 2x as the slow
4. The fast pointer is incremented to look ahead in the data structure to find the next element we want use
   1. Compare with the element at the slow pointer
   2. Replace the element at the slow pointer

Examples

1. Dealing with a loop in a linked list or array
2. Need to know the position of a certain element or the overall length of a linked list.
3. Moving elements ahead in an array
4. Trying to determine if a linked list is a palindrome
5. Dealing with cyclic linked lists or arrays.