A Red Black Tree is a self-balancing Binary Search Tree (BST) where each node has an extra bit for denoting the color of the node, either red or black. This color coding is used to ensure that the tree remains balanced during insertions and deletions.
Binary Search Tree (BST) performance can suffer if the tree becomes unbalanced. Red Black Tree are a type of balanced BST that use a set of rules to maintain balance, ensuring logarithmic time complexity for operations like insertion, deletion, and searching, regardless of the initial shape of the tree.
Why Red-Black Trees?
Most of the BST operations (e.g., search, max, min, insert, delete.. etc) take O(h) time where h is the height of the BST. The cost of these operations may become O(n) for a skewed Binary Tree If we make sure that the height of the tree remains O(log n) after every insertion and deletion, then we can guarantee an upper bound of O(log n) for all these operations. The height of a Red-Black tree is always O(log n) where n is the number of nodes in the tree.
Properties of Red-Black Trees
- Node Color: Each node is either red or black.
- Root Property: The root of the tree is always black.
- Red Property: Red nodes cannot have red children (no two consecutive red nodes on any path).
- Black Property: Every path from a node to its descendant null nodes (leaves) has the same number of black nodes.
- Leaf Property: All leaves (NIL nodes) are black.
These properties ensure that the longest path from the root to any leaf is no more than twice as long as the shortest path, maintaining the tree’s balance and efficient performance.
Example of Red-Black Tree:
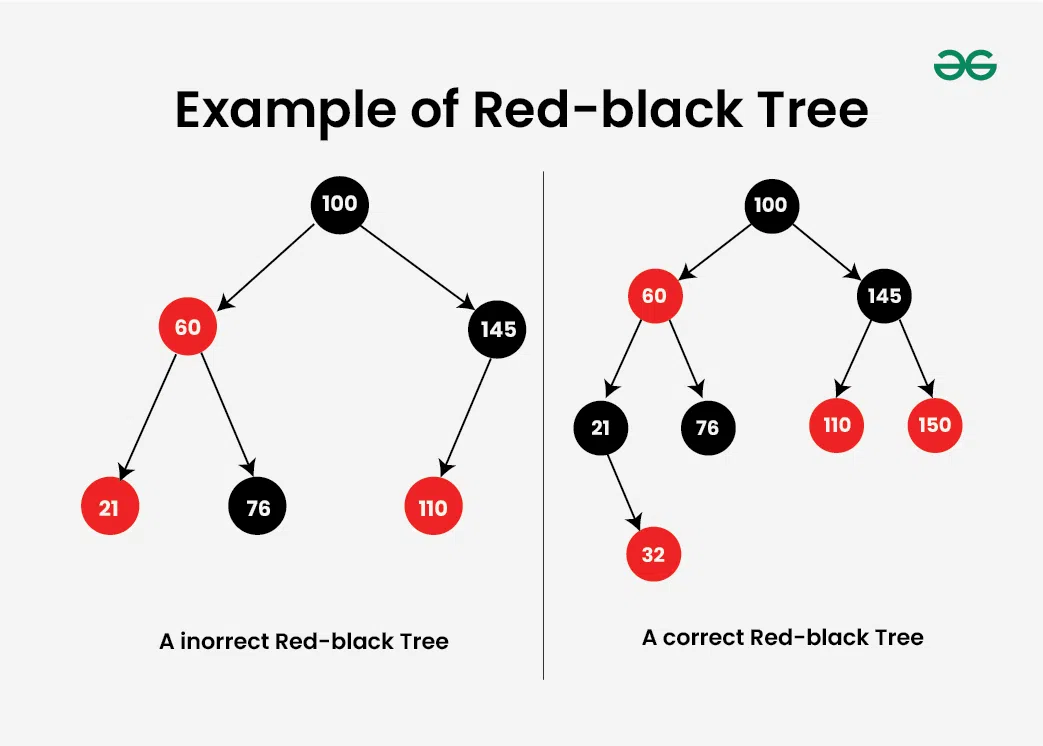
The Correct Red-Black Tree in above image ensures that every path from the root to a leaf node has the same number of black nodes. In this case, there is one (excluding the root node).
The Incorrect Red Black Tree does not follow the red-black properties as two red nodes are adjacent to each other. Another problem is that one of the paths to a leaf node has zero black nodes, whereas the other two contain a black node.
| Sr. No. | Algorithm | Time Complexity |
|---|---|---|
| 1. | Search | O(log n) |
| 2. | Insert | O(log n) |
| 3. | Delete | O(log n) |
How does a Red-Black Tree ensure balance?
A simple example to understand balancing is, that a chain of 3 nodes is not possible in the Red-Black tree. We can try any combination of colors and see if all of them violate the Red-Black tree property.
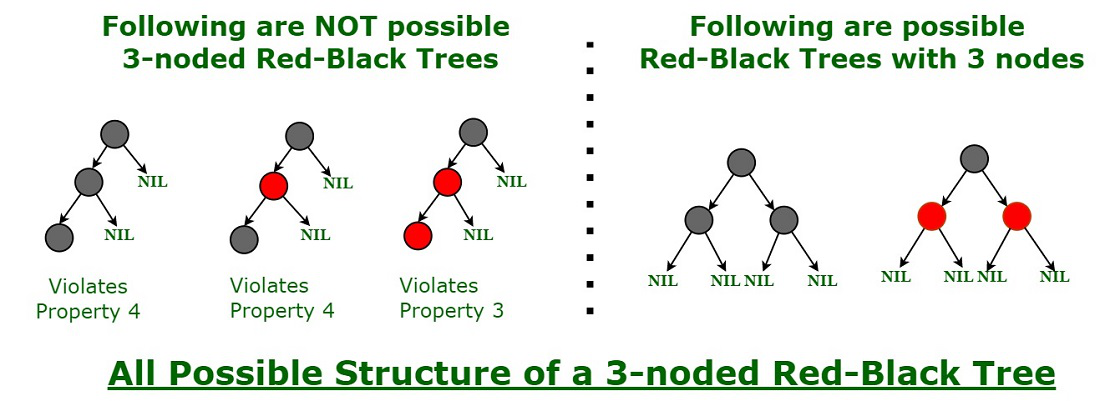
Proper structure of three noded Red-black tree
Interesting points about Red-Black Tree:
- The black height of the red-black tree is the number of black nodes on a path from the root node to a leaf node. Leaf nodes are also counted as black nodes. So, a red-black tree of height h has black height >= h/2.
- Height of a red-black tree with n nodes is h⇐ 2 log2(n + 1).
- All leaves (NIL) are black.
- The black depth of a node is defined as the number of black nodes from the root to that node i.e the number of black ancestors.
Advantages of Red-Black Trees:
- Balanced: Red-Black Trees are self-balancing, meaning they automatically maintain a balance between the heights of the left and right subtrees. This ensures that search, insertion, and deletion operations take O(log n) time in the worst case.
- Efficient search, insertion, and deletion: Due to their balanced structure, Red-Black Trees offer efficient operations. Search, insertion, and deletion all take O(log n) time in the worst case.
- Simple to implement: The rules for maintaining the Red-Black Tree properties are relatively simple and straightforward to implement.
- Widely used: Red-Black Trees are a popular choice for implementing various data structures, such as maps, sets, and priority queues.
Disadvantages of Red-Black Trees:
- More complex than other balanced trees: Compared to simpler balanced trees like AVL trees, Red-Black Trees have more complex insertion and deletion rules.
- Constant overhead: Maintaining the Red-Black Tree properties adds a small overhead to every insertion and deletion operation.
- Not optimal for all use cases: While efficient for most operations, Red-Black Trees might not be the best choice for applications where frequent insertions and deletions are required, as the constant overhead can become significant.
Applications of Red-Black Trees:
- Implementing maps and sets: Red-Black Trees are often used to implement maps and sets, where efficient search, insertion, and deletion are crucial.
- Priority queues: Red-Black Trees can be used to implement priority queues, where elements are ordered based on their priority.
- File systems: Red-Black Trees are used in some file systems to manage file and directory structures.
- In-memory databases: Red-Black Trees are sometimes used in in-memory databases to store and retrieve data efficiently.
- Graphics and game development: Red-Black Trees can be used in graphics and game development for tasks like collision detection and pathfinding.
Basic Operations of Red Black Tree in C++
Following are some of the basic operations of a Red Black Tree that are required to manipulate its elements:
| Operation | Description | Time Complexity | Space Complexity |
|---|---|---|---|
| Insert | Inserts a new element into the tree. | O(log n) | O(1) |
| Delete node | Removes an element from the tree. | O(log n) | O(1) |
| Search | Searches for an element in the tree. | O(log n) | O(1) |
| Left Rotate | Performs a left rotation on a given node. | O(1) | O(1) |
| Right Rotate | Performs a right rotation on a given node. | O(1) | O(1) |
Here, n represents the number of nodes in the red black tree.