Binary Tree

A non-linear hierarchical data structure in which each node has at most two children, referred to as the left and right child. The topmost node is the root node, and the nodes at the last level having no children are the leaf nodes.

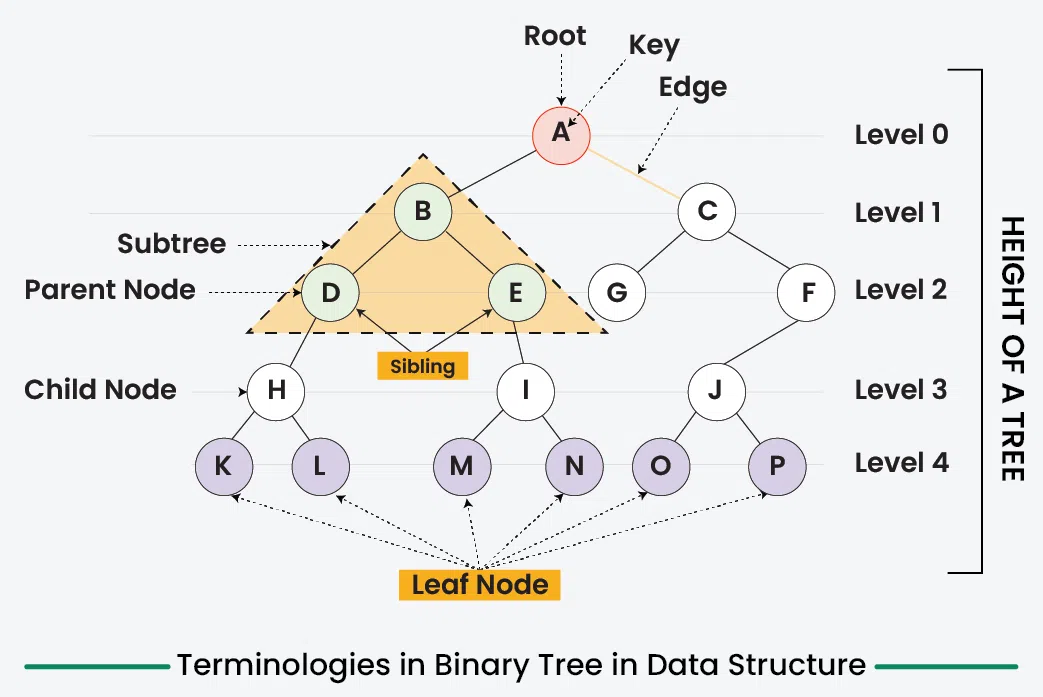
Terminology

• Nodes: The fundamental part of a binary tree. each node contains data and link to two child nodes.
• Root: The topmost node in a tree. It has no parent and serves as the starting point for all nodes.
• Parent Node: A node that has one or more child nodes. A node can have at most two children.
• Child Node: A node that is a descendant of another node.
• Leaf Node: A node that does not have any children or both children are null.
• Internal Node: A node that has at least one child. Includes all nodes except the root and the leaf nodes.
• Node Depth: The number of edges from a specific node to the root node. The depth of the root node is zero.
• Tree Height: The number of nodes from the deepest leaf node to the root node.

Properties

• The maximum number of nodes at level L of a binary tree is 2********L
• The maximum number of nodes in a binary tree of height H is 2********H – 1
• Total number of leaf nodes in a binary tree = total number of nodes with 2 children + 1
• In a Binary Tree with N nodes, the minimum possible height or the minimum number of levels is Log2(N+1)
• A Binary Tree with L leaves has at least | Log2L |+ 1 levels

Basic Operations

Operation Name	Description	Time Complexity	Space Complexity
Insertion	Inserts a new node into the binary tree.	O(N)	O(N)
Deletion	Deletes a specific node from the binary tree.	O(N)	O(N)
Search	Searches for a specific value in the binary tree.	O(N)	O(N)
Traversal	Inorder Traversal, Preorder Traversal, Postorder Traversal	O(N)	O(N)

Types

Binary Tree can be classified into multiples types based on multiple factors.

Number of Children

• Full Binary Tree: A full binary tree is a tree in which every node has either 0 or 2 children. In other words, all nodes except leaf nodes have two children.
• Degenerate Binary Tree: A degenerate binary tree is similar to a skewed binary tree. It’s a tree where each parent node has only one child node.
• Skewed Binary Tree: A skewed binary tree is a tree in which all nodes have only one child, either left or right. There are two types: left-skewed and right-skewed.

Completion of Levels

• Complete Binary Tree: A complete binary tree is a binary tree in which all levels are completely filled except possibly the last level, which is filled from left to right.
• Perfect Binary Tree: A perfect binary tree is a binary tree in which all interior nodes have two children and all leaves are at the same level.
• Balanced Binary Tree: A balanced binary tree is a binary tree in which the height of the left and right subtrees of every node differs by at most one.

Node Values

• Binary Search Tree: A Binary Search Tree is a binary tree where for each node, all elements in the left subtree are less than the node, and all elements in the right subtree are greater than the node.
• AVL Tree: An AVL tree is a self-balancing BST where the height of the left and right subtrees of any node differ by at most one.
• Red Black Tree: A Red-Black tree is a self-balancing BST where each node has an extra bit for denoting the color of the node, either red or black.
• B Tree: B-tree is a self-balancing tree data structure that maintains sorted data and allows searches, sequential access, insertions, and deletions in logarithmic time.
• B+ Tree: A B+ tree is a variant of the B-tree that has all data stored in the leaf nodes, while internal nodes only store keys.
• Segment Tree: A Segment Tree is a tree data structure used for storing information about intervals, or segments. It allows querying which of the stored segments contain a given point.
• Fenwick Tree: A Fenwick Tree is a data structure that can efficiently update elements and calculate prefix sums in a table of numbers.

Applications

• File System Organization: Represent hierarchical file structures. Each node in the tree represents a directory or a file, with the root node typically representing the main directory. Child nodes represent subdirectories or files within a directory.
• Expression Trees: In compilers and interpreters, expression trees are used to represent and evaluate arithmetic or logical expressions. Each internal node represents an operator (+, -, *, /, etc.), while leaf nodes represent operands (numbers or variables). This structure allows for easy parsing, evaluation, and optimization of mathematical expressions.
• Huffman Coding Trees: Huffman coding is a data compression algorithm that uses a binary tree structure. The tree is constructed based on the frequency of characters in the data. More frequent characters are assigned shorter codes, while less frequent ones get longer codes. This results in efficient data compression, especially for text files.
• Binary Search Tree (BST): BSTs are a special type of binary tree where for each node, all elements in the left subtree are smaller, and all elements in the right subtree are larger. This property makes BSTs extremely efficient for searching, insertion, and deletion operations, typically with O(log n) time complexity in balanced cases.
• Decision Trees: In machine learning, decision trees are used for classification and regression tasks. Each internal node represents a “test” on an attribute, each branch represents the outcome of the test, and each leaf node represents a class label or a numerical output. Decision trees are popular due to their interpretability and ability to handle both numerical and categorical data.
• Game Trees: In artificial intelligence, particularly for game strategy planning, game trees represent all possible moves and their outcomes in a game. Each level of the tree represents a player’s turn, and leaf nodes represent final game states
• Syntax Trees: Compilers use syntax trees (also known as abstract syntax trees or ASTs) to represent the structure of program code. Each node in the tree represents a construct in the source code, such as functions, loops, or conditional statements. This representation helps in code analysis, optimization, and generation of machine code.
• Priority Queue is another application of binary tree that is used for searching maximum or minimum in O(1) time complexity.
• Useful for indexing segmented at the database is useful in storing cache in the system

Advantages

Advantages

• Efficient Search: Binary Search Tree (BST)
• Memory Efficient: Require lesser memory as compared to other tree data structures.
• Relatively easy to implement and understand as each node has at most two children.

Disadvantages

• Limited structure: Limited to two child nodes per node, which limits their usefulness. For example, if a tree requires more than two child nodes per node, a different tree structure may be more suitable.
• Unbalanced trees: Unbalanced binary trees, where one subtree is significantly larger than the other, can lead to inefficient search. This can occur if the tree is not properly balanced or if data is inserted in a non-random order.
• Space inefficiency: Can be space inefficient when compared to other data structures like arrays and linked list. Because each node requires two child references or pointers, which can be a significant amount of memory overhead for large trees.
• Slow performance in worst-case scenarios: In the worst-case scenario, a binary tree can become degenerate or skewed, meaning that each node has only one child. In this case, search operations in Binary Search Tree (BST) can degrade to O(n) time complexity.

Implementation

To implement a binary tree, we use a node-based approach. Each node of the binary tree will contain data and pointers to its left and right children.

C++

// Use any below method to implement Nodes of binary tree
 
// 1: Using struct
struct Node {
    int data;
    Node* left, * right;
 
    Node(int key) {
        data = key;
        left = nullptr;
        right = nullptr;
    }
};
 
// 2: Using class
class Node {
public:
    int data;
    Node* left, * right;
 
    Node(int key) {
        data = key;
        left = nullptr;
        right = nullptr;
    }
};
 
// 3: Using template class
template <typename T>  
class Node {  
public:  
    T data;  
    Node* left;  
    Node* right;
    Node (T value): data(value), left(nullptr), right(nullptr) {}
};

// C++ Program for Implementing Binary Tree
#include <iostream>
#include <queue>
using namespace std;
 
// Template class for the Node of a Binary Tree
template <typename T>
class Node {
public:
    // Data held by the node
    T data;  
    // Pointer to the left child
    Node* left;  
    // Pointer to the right child
    Node* right;  
    // Constructor to initialize the node with a value
    Node(T value) : data(value), left(nullptr), right(nullptr) {}
};
 
// Template class for a Binary Tree
template <typename T>
class BinaryTree {
private:
    // Pointer to the root of the tree
    Node<T>* root;  
 
    // Recursive Function to delete a node from the tree
    Node<T>* deleteRecursive(Node<T>* current, T value) {
        if (current == nullptr) return nullptr;
 
        if (current->data == value) {
            if (current->left == nullptr && current->right == nullptr) {
                delete current;
                return nullptr;
            }
            if (current->left == nullptr) {
                Node<T>* temp = current->right;
                delete current;
                return temp;
            }
            if (current->right == nullptr) {
                Node<T>* temp = current->left;
                delete current;
                return temp;
            }
 
            Node<T>* successor = findMin(current->right);
            current->data = successor->data;
            current->right = deleteRecursive(current->right, successor->data);
        } else {
            current->left = deleteRecursive(current->left, value);
            current->right = deleteRecursive(current->right, value);
        }
        return current;
    }
 
    // Helper Function to find the minimum value node
    Node<T>* findMin(Node<T>* node) {
        while (node->left != nullptr) node = node->left;
        return node;
    }
 
    // Recursive Function to search for a value in the tree
    bool searchRecursive(Node<T>* current, T value) {
        if (current == nullptr) return false;
        if (current->data == value) return true;
        return searchRecursive(current->left, value) || searchRecursive(current->right, value);
    }
 
    // Function for Recursive inorder traversal of the tree
    void inorderRecursive(Node<T>* node) {
        if (node != nullptr) {
            inorderRecursive(node->left);
            cout << node->data << " ";
            inorderRecursive(node->right);
        }
    }
 
    // Function for Recursive preorder traversal of the tree
    void preorderRecursive(Node<T>* node) {
        if (node != nullptr) {
            cout << node->data << " ";
            preorderRecursive(node->left);
            preorderRecursive(node->right);
        }
    }
 
    // Function for Recursive postorder traversal of the tree
    void postorderRecursive(Node<T>* node) {
        if (node != nullptr) {
            postorderRecursive(node->left);
            postorderRecursive(node->right);
            cout << node->data << " ";
        }
    }
 
public:
    // Constructor to initialize the tree
    BinaryTree() : root(nullptr) {}
 
    // Function to insert a node in the binary tree 
    void insertNode(T value) {
        Node<T>* newNode = new Node<T>(value);
 
        if (root == nullptr) {
            root = newNode;
            return;
        }
 
        queue<Node<T>*> q;
        q.push(root);
 
        while (!q.empty()) {
            Node<T>* current = q.front();
            q.pop();
 
            if (current->left == nullptr) {
                current->left = newNode;
                return;
            } else {
                q.push(current->left);
            }
 
            if (current->right == nullptr) {
                current->right = newNode;
                return;
            } else {
                q.push(current->right);
            }
        }
    }
 
    // Function to delete a node from the tree
    void deleteNode(T value) {
        root = deleteRecursive(root, value);
    }
 
    // Function to search for a value in the tree
    bool search(T value) {
        return searchRecursive(root, value);
    }
 
    // Function to perform inorder traversal of the tree
    void inorder() {
        inorderRecursive(root);
        cout << endl;
    }
 
    // Function to perform preorder traversal of the tree
    void preorder() {
        preorderRecursive(root);
        cout << endl;
    }
 
    // Function to perform postorder traversal of the tree
    void postorder() {
        postorderRecursive(root);
        cout << endl;
    }
 
    // Function  to perform level order traversal of the tree
    void levelOrder() {
        if (root == nullptr) return;
 
        queue<Node<T>*> q;
        q.push(root);
 
        while (!q.empty()) {
            Node<T>* current = q.front();
            q.pop();
 
            cout << current->data << " ";
 
            if (current->left != nullptr) q.push(current->left);
            if (current->right != nullptr) q.push(current->right);
        }
        cout << endl;
    }
};
 
int main() {
    BinaryTree<int> tree;
    
    // Insert the nodes into the tree
    tree.insertNode(1);
    tree.insertNode(2);
    tree.insertNode(3);
    tree.insertNode(4);
    tree.insertNode(5);
    tree.insertNode(6);
 
    cout << "Inorder traversal: ";
    tree.inorder();
 
    cout << "Preorder traversal: ";
    tree.preorder();
 
    cout << "Postorder traversal: ";
    tree.postorder();
 
    cout << "Level order traversal: ";
    tree.levelOrder();
 
    cout << "Searching for 7: " << (tree.search(7) ? "Found" : "Not Found") << endl;
    cout << "Searching for 6: " << (tree.search(6) ? "Found" : "Not Found") << endl;
 
    tree.deleteNode(3);
    cout << "Inorder traversal after removing 3: ";
    tree.inorder();
 
    return 0;
}