94. Binary Tree Inorder Traversal

Problem

Given the root of a binary tree, return the inorder traversal of its nodes’ values.

Example 1: Input: root = [1,null,2,3] Output: [1,3,2] Explanation:

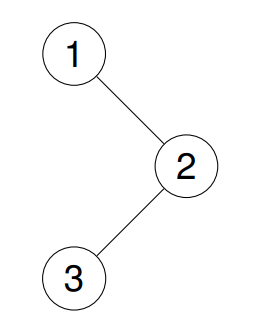
Example 2: Input: root = [1,2,3,4,5,null,8,null,null,6,7,9] Output: [4,2,6,5,7,1,3,9,8] Explanation:

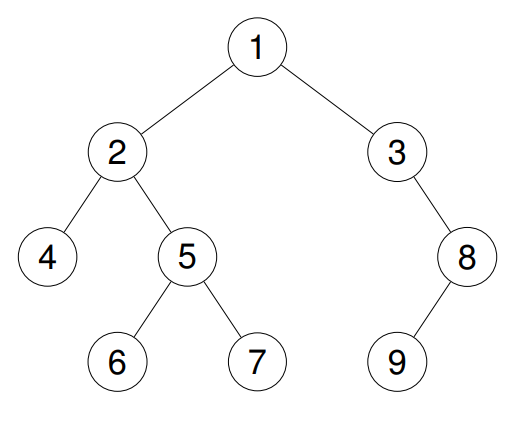
Example 3: Input: root = [] Output: []

Example 4: Input: root = [1] Output: [1]

Constraints:

• The number of nodes in the tree is in the range [0, 100].
• -100 <= Node.val <= 100

Follow up: Recursive solution is trivial, could you do it iteratively?

Solution

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

Recursion - O(n) time - O(n) space

class Solution {
public:
    vector<int> result;
    vector<int> inorderTraversal(TreeNode* root) {
        if (!root) return vector<int>();
        inorderTraversal(root->left);
        result.push_back(root->val);
        inorderTraversal(root->right);
        return result;
    }
};

Stack - O(n) time - O(n) space

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> stack;
        TreeNode* curr = root;
 
        while (curr != NULL || !stack.empty()) {
            while (curr != NULL) {
                stack.push(curr);
                curr = curr->left;
            }
            curr = stack.top();
            stack.pop();
            res.push_back(curr->val);
            curr = curr->right;
        }
        return res;
    }
};

Morris Traversal - O(n) time - O(1) space

Using a Threaded Binary Tree.

1. Initialize current as root
2. While current is not NULL
   1. If current does not have left child
      1. Add current’s value
      2. Go to the right, i.e., current = current.right
   2. Else
      1. In current’s left subtree, make current the right child of the rightmost node
      2. Go to this left child, i.e., current = current.left

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        TreeNode* curr = root;
        TreeNode* pre;
 
        while (curr != nullptr) {
            if (curr->left == nullptr) {
                res.push_back(curr->val);
                curr = curr->right;  // move to next right node
            } else {
                pre = curr->left;
                while (pre->right != nullptr && pre->right != curr) {  // find rightmost
                    pre = pre->right;
                }
 
                if (pre->right == nullptr) {
                    // establish a link back to the current node
                    pre->right = curr;
                    curr = curr->left;
                } else {
                    // restore the tree structure
                    pre->right = nullptr;
                    res.push_back(curr->val);
                    curr = curr->right;
                }
            }
        }
        return res;
    }
};