Problem
Given the root of a binary tree, return the postorder traversal of its nodes’ values.
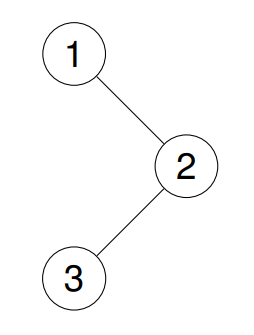
Example 1: Input: root = [1,null,2,3] Output: [3,2,1] Explanation:
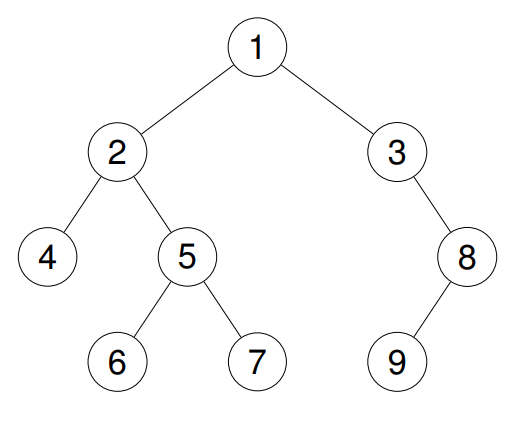
Example 2: Input: root = [1,2,3,4,5,null,8,null,null,6,7,9] Output: [4,6,7,5,2,9,8,3,1] Explanation:
Example 3: Input: root = [] Output: []
Example 4: Input: root = [1] Output: [1]
Constraints:
- The number of the nodes in the tree is in the range
[0, 100]. -100 <= Node.val <= 100
Follow up: Recursive solution is trivial, could you do it iteratively?
Solution
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/Recursion - O(n) time - O(n) space
class Solution {
public:
vector<int> result;
vector<int> postorderTraversal(TreeNode* root) {
if (!root) return vector<int>();
postorderTraversal(root->left);
postorderTraversal(root->right);
result.push_back(root->val);
return result;
}
};class Solution {
public:
void postorderTraversalHelper(TreeNode* currentNode, vector<int>& result) {
if (!currentNode) {
return;
}
postorderTraversalHelper(currentNode->left, result);
postorderTraversalHelper(currentNode->right, result);
result.push_back(currentNode->val);
}
vector<int> postorderTraversal(TreeNode* root) {
vector<int> result;
postorderTraversalHelper(root, result);
return result;
}
};Reverse Preorder Traversal- O(n) time - O(n) space
Exploiting the relationship between preorder and postorder traversals. In a standard preorder traversal, we visit the root node before we visit the left and right subtrees. However, postorder traversal requires us to visit the left and right subtrees before the root node.
We can adapt the preorder traversal by visiting nodes in the order of root, right subtree, and then left subtree. Reversing the resulting list from this modified preorder traversal gives us the correct postorder sequence.
We use a stack to traverse the tree iteratively, starting with the root node. We push the current node onto the stack and add its value to the result list. Instead of moving to the left child, we move to the right child. If there’s no right child, we pop a node from the stack and move to its left child. This approach processes the right subtree before the left subtree, aligning with the modified preorder traversal.
After traversing the entire tree, we reverse the result list to get the postorder sequence: left subtree, right subtree, root.
Algorithm
- Initialize an empty
resultlist to store the traversal result, atraversalStackfor nodes, and setcurrentNodetoroot. - While
currentNodeis notnullortraversalStackis not empty:- If
currentNodeis notnull, addcurrentNode->valto theresultlist before processing its children. - Push
currentNodeonto thetraversalStackto revisit it later. - Move
currentNodetocurrentNode->rightto continue traversal in the right subtree. - If
currentNodeisnull, pop the top node fromtraversalStackand set it tocurrentNode. - Move
currentNodetocurrentNode->leftto process the left subtree.
- If
- Reverse the
resultlist to correct the order from preorder to postorder. - Return the
resultlist with postorder traversal values.
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
// Vector to store the result of postorder traversal
vector<int> result;
// Stack to facilitate the traversal of nodes
stack<TreeNode*> traversalStack;
TreeNode* currentNode = root;
// Traverse the tree while there are nodes to process
while (currentNode != nullptr || !traversalStack.empty()) {
if (currentNode != nullptr) {
// Add current node's value to result list before going to its
// children
result.push_back(currentNode->val);
// Push current node onto the stack
traversalStack.push(currentNode);
// Move to the right child
currentNode = currentNode->right;
} else {
// Pop the node from the stack and move to its left child
currentNode = traversalStack.top();
traversalStack.pop();
currentNode = currentNode->left;
}
}
// Reverse the result list to get the correct postorder sequence
reverse(result.begin(), result.end());
return result;
}
};Two Stack - O(n) time - O(n) space
We use two stacks to control the node processing order systematically.
First, we push the root node onto the first stack. This stack simulates the recursive traversal of the tree. To process nodes in postorder (left-right-root), we need a second stack to reverse the order. As we pop nodes from the first stack, we push them onto the second stack. This reversal ensures that nodes are processed in the correct order.
After all nodes are transferred to the second stack, popping from it gives us the nodes in postorder sequence. This method efficiently achieves the desired traversal order by leveraging the two stacks to manage the processing sequence without needing a final reversal step.
Algorithm
- Initialize an empty
resultlist, and createmainStackandpathStackfor nodes. - Check if
rootisnull; if so, returnresultimmediately, indicating there are no nodes to process. - Push
rootontomainStackto start the traversal. - While
mainStackis not empty:- Peek at the top of
mainStackto examine the current node. - If the top of
pathStackis the same as the top ofmainStack, addroot->valto theresultlist. - Pop the top node from both
mainStackandpathStackafter processing. - Otherwise, push the current node onto
pathStack. - Push
root->rightandroot->leftontomainStackif they exist to process their children.
- Peek at the top of
- Return the
resultlist containing postorder traversal values.
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> result;
// If the root is null, return an empty list
if (!root) return result;
// Stack to manage the traversal
stack<TreeNode*> mainStack;
// Stack to manage the path
stack<TreeNode*> pathStack;
// Start with the root node
mainStack.push(root);
// Process nodes until the main stack is empty
while (!mainStack.empty()) {
root = mainStack.top();
// If the node is in the path stack and it's the top, add its value
if (!pathStack.empty() && pathStack.top() == root) {
result.push_back(root->val);
mainStack.pop();
pathStack.pop();
} else {
// Push the current node to the path stack
pathStack.push(root);
// Push right child if it exists
if (root->right) mainStack.push(root->right);
// Push left child if it exists
if (root->left) mainStack.push(root->left);
}
}
return result;
}
};Stack - O(n) time - O(n) space
We can use a single stack combined with a previousNode pointer to track the traversal.
We start by pushing nodes onto the stack while traversing left, similar to inorder traversal. In postorder traversal, we must process each node after its right subtree. To manage this, the previousNode pointer helps remember the last processed node.
When a node is reached on the stack, we first check if it has an unvisited right child. If so, we move to that right child since we can’t process the current node until after its right subtree. If the node has no right child or its right child has already been processed (indicated by previousNode), we process the node by popping it from the stack and adding its value to the result list, then update previousNode to this node.
Algorithm
- Initialize an empty
resultlist, setpreviousNodetonull, and initializetraversalStack. - Check if
rootisnull; if so, returnresultimmediately, indicating there are no nodes to process. - While
rootis notnullortraversalStackis not empty:- If
rootis notnull, pushrootontotraversalStack. - Move
roottoroot->leftto process the left subtree. - If
rootisnull, peek at the top oftraversalStack. - If
root->rightisnullorroot->rightequalspreviousNode, addroot->valtoresult. - Pop
rootfromtraversalStack, setpreviousNodetoroot, and setroottonull. - If
root->rightis notnull, moveroottoroot->rightto continue the traversal.
- If
- Return the
resultlist containing postorder traversal values.
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> result;
// If the root is null, return an empty list
if (root == nullptr) return result;
// To keep track of the previously processed node
TreeNode* previousNode = nullptr;
// Stack to manage the traversal
stack<TreeNode*> traversalStack;
// Process nodes until both the root is null and the stack is empty
while (root != nullptr || !traversalStack.empty()) {
// Traverse to the leftmost node
if (root != nullptr) {
traversalStack.push(root);
root = root->left;
} else {
// Peek at the top node of the stack
root = traversalStack.top();
// If there is no right child or the right child was already
// processed
if (root->right == nullptr || root->right == previousNode) {
result.push_back(root->val);
traversalStack.pop();
previousNode = root;
root = nullptr; // Ensure we don’t traverse again from this
// node
} else {
// Move to the right child
root = root->right;
}
}
}
return result;
}
};Morris Traversal - O(n) time - O(1) space
In Morris traversal, the tree structure is temporarily modified to create temporary links that simulate the effect of a stack or recursion. As a result, there is no overhead from additional data structures and the space complexity is constant. The high level idea is to link each predecessor back to the current node, which allows us to trace back to the top of the tree.
We introduce a dummyNode with a value that is not part of the original tree and link it to the root. Our traversal begins with this dummyNode, treating it as the new root of the tree.
For each node, we look for its in-order predecessor, the rightmost node in its left subtree. We do this so that the in-order predecessor can be used to create a temporary link back to the current node, simulating the recursive call stack.
- If the current node has a left child, we find the rightmost node in the left subtree. This rightmost node is the in-order predecessor.
- We then create a temporary link from this predecessor to the current node by setting its right pointer to the current node.
If the predecessor’s right pointer is null, set it to point to the current node and move to the left child. This simulates the recursive call by allowing us to return to the current node after processing the left subtree.
When a node’s predecessor’s right pointer points back to the current node, it indicates the left subtree is processed. Process the current node and reverse the temporary link to restore the tree’s structure.
Finally, move to the right child and continue the traversal.
Morris traversal operates in O(n) time because finding the predecessor is not done for every node but only for nodes with a valid left child.
Algorithm
- Initialize an empty
resultlist and create a dummy node with the value-1. SetdummyNode->lefttorootand updateroottodummyNode. - Check if
rootisnull; if so, returnresultimmediately, indicating there are no nodes to process. - While
rootis notnull:- If
root->leftis notnull, find the rightmost node (predecessor) in theroot->leftsubtree. - If the right child of the predecessor is
null, set the right child torootand moveroottoroot->left. - If the right child of the predecessor is
root, perform reverse traversal of theroot->leftsubtree and add values toresult. - Reverse the subtree back to its original state by restoring pointers.
- Remove the temporary link from the predecessor to
rootand moveroottoroot->right. - If
root->leftisnull, moveroottoroot->right.
- If
- Return the
resultlist containing postorder traversal values.
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> result;
// If the root is null, return an empty list
if (root == NULL) return result;
// Create a dummy node to simplify edge cases
TreeNode dummy = -1;
TreeNode* dummyNode = &dummy;
TreeNode* predecessor = NULL;
dummyNode->left = root;
root = dummyNode;
// Traverse the tree
while (root != NULL) {
// If the current node has a left child
if (root->left != NULL) {
predecessor = root->left;
// Find the rightmost node in the left subtree or the thread
// back to the current node
while (predecessor->right != NULL &&
predecessor->right != root) {
predecessor = predecessor->right;
}
// Create a thread if it doesn't exist
if (predecessor->right == NULL) {
predecessor->right = root;
root = root->left;
} else {
// Process the nodes in the left subtree
TreeNode* node = predecessor;
reverseSubtreeLinks(root->left, predecessor);
// Add nodes from right to left
while (node != root->left) {
result.push_back(node->val);
node = node->right;
}
result.push_back(node->val); // Add root.left's value
reverseSubtreeLinks(predecessor, root->left);
predecessor->right = NULL;
root = root->right;
}
} else {
// Move to the right child if there's no left child
root = root->right;
}
}
return result;
}
void reverseSubtreeLinks(TreeNode* startNode, TreeNode* endNode) {
if (startNode == endNode) {
return; // If the start and end nodes are the same, no need to
// reverse
}
TreeNode* prev = NULL;
TreeNode* current = startNode;
TreeNode* next = NULL;
// Reverse the direction of the pointers in the subtree
while (current != endNode) {
next = current->right;
current->right = prev;
prev = current;
current = next;
}
// Reverse the last node
current->right = prev;
}
};